Математические функции

• Повторение: создание исполняемой программы из исходного кода на Си:

  1. Трансляция: файл на Си → объектный файл (все операторы Си переведены на машинный язык)
  2. Компоновка: объектный файл → исполняемый файл (к объектному файлу добавлена исполняющая подсистема Си и другие подпрограммы, непосредственно либо в виде указания библиотеки, откуда эти подпрограммы может загрузить операционная система)

• Вот здесь более подробный рассказ о компоновке: FrBrGeorge/LinkingC

• Использование математических функций:

  • В начале программы — #include <math.h>; в этом файле содержатся описания математических функций

  • В тексте программы можно использовать функции из списка, например, так:

       1 #include <stdio.h>
       2 #include <math.h>
       3 
       4 void main() {
       5     float a, b, c, p;
       6     printf("Введите стороны треугольника a b c: ");
       7     scanf("%f %f %f", &a, &b, &c);
       8     p = (a+b+c)/2;
       9     printf("Площадь треугольника по формуле Горона: %f\n", sqrt((p-a)*(p-b)*(p-c)*p));
      10 }
    

• здесь должен был быть рассказ про atan2(), но тригонометрия была не у всех

• Подключение математической библиотеки при компиляции в geany:

  открыть любой файл на Си и вызвать «Сборка ⇒ Установить команды сборки»

  • 

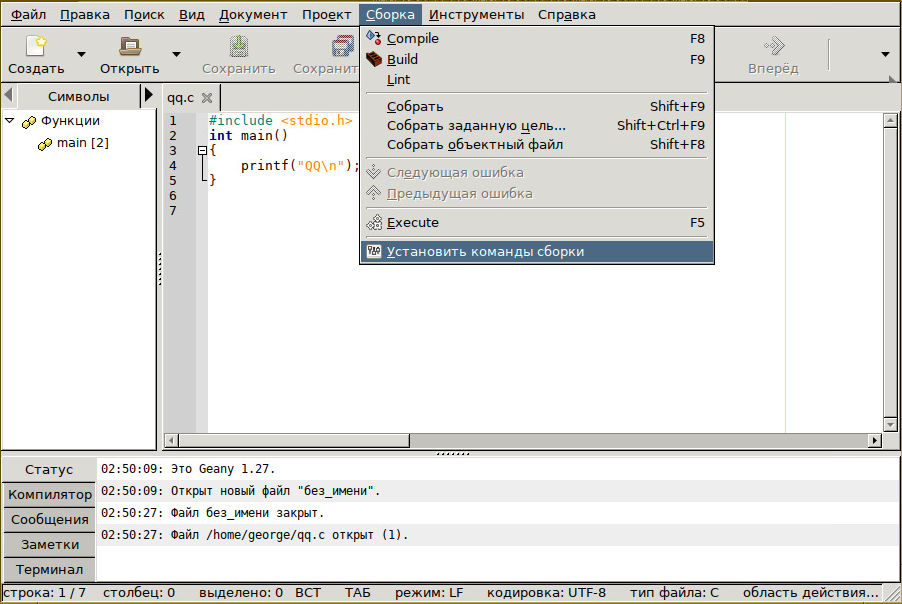
    • Выставить " -lm" в конце каждой команды сборки, если там этой строеи нет

    

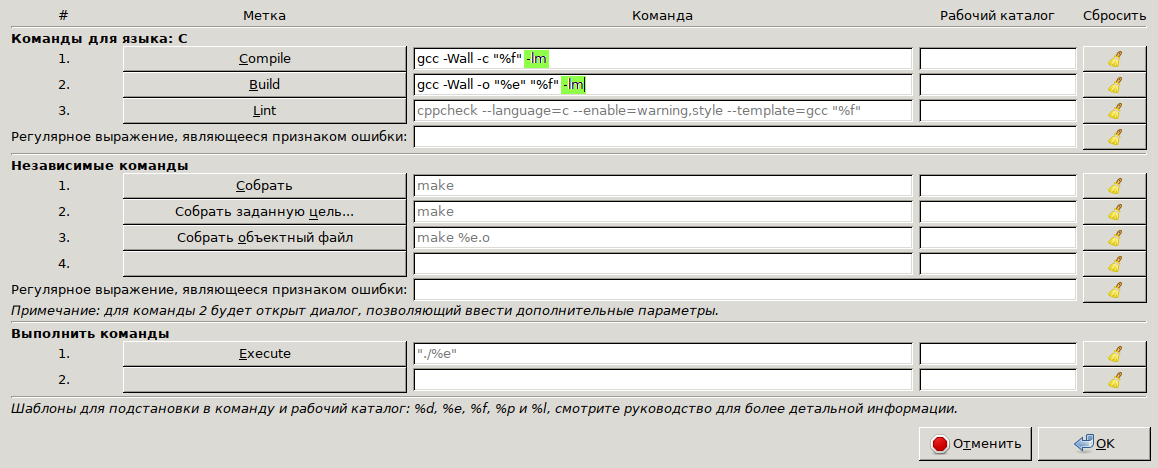
• Цикл по вводу с маркером конца. Например, вводятся пары чисел, а конец ввода — не пара чисел. Воспользуемся свойством функции scanf() не выдавать ошибки, а только возвращать количество успешно введённых переменных:

     1 #include <stdio.h>
     2 
     3 void main() {
     4     int a, b;
     5 
     6     while(scanf("%d %d", &a, &b)==2)
     7       printf("Введено %d и %d\n", a, b);
     8 }
  

  • Короткая и удобная запись. Использование тоже удобное: просто вводим мусор вместо пары чисел.

• Разбор задачи №3 прошлого Д/З:

Домашнее задание

0. Прочитать про функции libm из учебника (более подробно см. тут).

1. Настроить сборочное окружение (см. выше), чтобы при сборке подключалась библиотека m

2. (упражнение) Вводятся тройки вещественных чисел через пробел. Считая эти тройки сторонами параллелепипеда, найти наибольшее значение его диагонали. Конец ввода — любая строка, не являющаяся числом.
3. Ввести 8 чисел — координаты точек A, B, X, и Y. Проверить, лежат ли точки X и Y в одной полуплоскости относительно прямой, проходящей через A и B

4. Пары кубов. Ввести натуральное число N. Проверить, можно ли представить это число в виде суммы кубов двух неотрицательных целых чисел.

   • Обязательно сделать эту задачу простым методом (вложенные циклы) в качестве упражнения

   • Подсказка. Для для любого A, такого что $$ A < root(3)(N) $$, из всех вариантов B интересно проверить только два, такие, что $$A^3+B^3<=N$$, а $$A^3+(B+1)^3>=N$$. Остальные значения: $$A^3+(B-1)^3$$ и $$A^3+(B+2)^3$$, очевидно, не подойдут сразу.

     • Придумать более эффективный метод решения задачи

• CategoryClasses