Цилкы (2): break и continue

• Разбор домашних заданий
• Например: «Ввести натуральное число n. Поменять порядок цифр числа n на обратный»

  • Вариант с while (фрагмент)

       1   res = 0;
       2   while(n>0) {
       3     res = res * 10 + n%10;
       4     n/=10;
       5   }                 
    

    Обратите внимание на чёткие четыре части чанонической чхемы чикла

  • Вариант с for (очевиден)

       1   for(res = 0; n>0; n/=10)
       2     res = res * 10 + n%10;
    

• «Найти в последовательности натуральных чисел, заканчивающейся 0, число, превосходящее 20, и вывести его, иначе ничего не выводить»

  • Неправильное решение (с выводом всех чисел >20, а не первого)

       1   int n;
       2 
       3   scanf("%d",&n);
       4   while(n!=0) {
       5     if(n>20)
       6       printf("%d\n",n);
       7     scanf("%d",&n);
       8   }
    

  • Условие n>20 можно ввести в качестве дополнительного условия в цикле (while(n!=0 && n<20), но:

    • Это слегка запутывает код: последовательность заканчивается нулём, а по n>20 мы выходим, потому что искать больше не надо

    • По окончании цикла придётся ещё раз проверять значение n, чтобы его вывести

  • Если программа встречает оператор break, цикл немедленно завершается, и вычисление продолжается после его конца:

       1   int n;
       2 
       3   scanf("%d",&n);
       4   while(n!=0) {
       5     if(n>20) {
       6       printf("%d\n",n);
       7       break;
       8     }
       9     scanf("%d",&n);
      10   }
    

• Усложним задачу «Найти в последовательности натуральных чисел, заканчивающейся 0, число k, для которого верно неравенство 111.0/(40-2*k)>1, и вывести его». (111.0 вместо 111 используется для того, чтобы деление было вещественным, а не целочисленным).

  • Неправильное решение (найдите ошибку!):

       1   int n;
       2 
       3   scanf("%d",&n);
       4   while(n!=0) {
       5     if(111.0/(40-2*n)>1) {
       6       printf("%d\n",n);
       7       break;
       8     }
       9     scanf("%d",&n);
      10   }
    

  • Если программа встречает оператор continue, выполнение переходит сразу к проверке условия (то есть начинается следующий оборот цикла):

       1   int n;
       2 
       3   scanf("%d",&n);
       4   while(n!=0) {
       5     if (40-2*n == 0)
       6       continue;
       7     if(111.0/(40-2*n)>1) {
       8       printf("%d\n",n);
       9       break;
      10     }
      11     scanf("%d",&n);
      12   }
    

  • На самом деле можно было воспользоваться свойством неполного вычисления логических операций, и написать так:

       1     if (40-2*n !=0 && 111.0/(40-2*n)>1) {
       2       printf("%d\n",n);
       3       break;
       4     }
    

    • Вторая часть дизъюнкции не будет даже вычисляться, если первая уже ложь.

Домашнее задание

0. Прочитать в учебнике пример программы с циклом while и использование цикла for

1. Числа Фибоначчи. Пусть f₀=f₁=1; f₂=f₁+f₀=2; f₃=f₂+f₁=3; f₄=f₃+f₂=5; f₅=f₄+f₃=8; … ; f_n=f_n-1+f_n-2; … . Ввести n, вывести f_n .

2. Вычислить бесконечную сумму с заданной точностью ε (ε > 0). Считать, что требуемая точность достигнута, если вычислена сумма нескольких первых слагаемых, и очередное слагаемое оказалось по модулю меньше, чем ε (тогда это и все последующие слагаемые можно уже не учитывать).

   • Число ε ввести в переменную eps, вычислить: ,

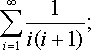     • то есть 1/(1*(1+1)) + 1/(2*(2+1)) + 1/(3*(3+1))+…

     Замечание: деление должно быть не целочисленным

3. Алгоритм Евклида нахождения наибольшего общего делителя (НОД) неотрицательных целых чисел основан на следующих свойствах этой величины. Пусть m и n — одновременно не равные нулю целые неотрицательные числа, и пусть m ≥ n. Тогда, если n == 0, то НОД(n, m) = m, а если n ≠ 0, то для чисел m, n и r, где r — остаток от деления m на n, выполняется равенство НОД(m, n) = НОД(n, r). Например, НОД(15, 6) = НОД(6, 3) = НОД(3, 0) = 3. Ввести натуральные числа n, m (m ≥ n), вывести наибольший общий делитель n и m.

4. Ввести натуральное число n. Вычислить: 1*2 + 2*3*4 + ... + n*(n+1)*...*2n.

   • Вариант: сделать это в одном цикле, без вложенных

CategoryClasses