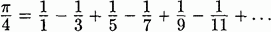Рекурсия и итераторы

Долги за прошлый раз

• Ещё раз про eval(input())

• Ещё раз про операцию () + про callable() и __call__()

Про рекурсию

• Рекурсия и цикл. Теория vs. практика. Гвидо, Python и хвостовой вызов

  • ⇒ максимальная глубина рекурсии
  • ⇒ логарифмический критерий уместности рекурсии

• Замещение рекурсии стеком. Пример: есть ли среди натуральных чисел Seq такие, что в сумме дают S. Рекурсивный вариант.

  •    1 def subsumR(S, Seq, Res=[]):
       2     if sum(Res) == S:
       3         return Res
       4     for i, el in enumerate(Seq):
       5         R = subsumR(S, Seq[i+1:], Res+[el])
       6         if R: return R
       7     return []
    

    S — неизменяемая часть, Seq, Res — изменяемая, значит, их надо сохранять в стек. Рекурсия — это цикл, которые продолжается до тех пор, пока рекурсивные вызовы не кончились.

       1 def subsumS(S, Num):
       2     Stack = [(Num,[])]
       3     while Stack:
       4         Seq, Res = Stack.pop()
       5         if sum(Res) == S:
       6             return Res
       7         Stack.extend((Seq[i+1:], Res+[el]) for i, el in enumerate(Seq))
       8     return []
    

    (здесь не тот порядок добавления, для полного соответствия надо в обратном)

Про генераторы

Вычислимые последовательности.

• Как задать самому? Например, циклической сборкой, см. пример выше

• iterator object, next(), StopIteration

• протокол последовательности: методы .__getitem__() или .__iter__()

  • iter() от всего подряд

  • ⇒ работа цикла for: сделать итератор и по нему ходить

• Создание и использование генератора, (yield ⇒ функция, возвращающая генератор, а уж генератор yield-ит результаты)

  • Пример работы, return в генераторе

  • Генератор — «одноразовая» последовательность

  • yield from, важность этой конструкции

Itertools (сколько успеем)

Бесконечные последовательности и частичные вычисления, itertools

• Обработка вычислимых последовательностей
• функциональное программирование
• Обзор
  • Бесконечные последовательности
  • Модификация последовательностей
  • Комбинаторика

Д/З

TODO

0. Прочитать что Гвидо думает о хвостовых рекурсивных вызовах, про итераторы и генераторы, про yield from и про itertools

1. (это не рекурсия, а вот итератор применить можно ☺)

   EJudge: UniInterval 'Объединение отрезков'

   Вводится кортеж пар натуральных чисел. Это координаты отрезков на прямой. Рассмотрим объединение этих отрезков и найдём длину этого объединения (т. е. совокупную длину всех «закрашенных» нашими отрезками отрезков на прямой).

   Input:

   (66, 91), (152, 230), (21, 81), (323, 342), (158, 211), (286, 332), (294, 330), (18, 58), (183, 236)

   Output:

   213

2. EJudge: BinPow 'Бинарное возведение в степень'

   Написать рекурсивную функцию BinPow(), которая принимает три параметра: python3-объект a, натуральное число 0<N<1000000, и некоторую ассоциативную бинарную функциюf(). Функция BinPow() реализует алгоритм бинарного возведения в степень (кроме нулевой степени). Результатом BinPow(a, n, f) будет применение f(x) к a n-1 раз. Более точно, BinPow(a, 1, f) == a, BinPow(a, 2, f) == f(a,a), BinPow(a, 3, f) == f(a,f(a, a)) == f(f(a, a), a) (в силу ассоциативности), … BinPow(a, n, f) == f(f(…f(a, a), …), a).

   Input:

   print(BinPow(2,33,int.__mul__), 2**33)
   print(BinPow("Se", 7, str.__add__))

   Output:

   8589934592 8589934592
   SeSeSeSeSeSeSe

3. EJudge: IterPi 'Пи /кродёться/'

   Пользуясь формулой Лейбница для вычисления числа Пи:

   • 

   написать бесконечный генератор pigen(), возвращающий последовательно 4, 4-4/3, 4-4/3+4/5, 4-4/3+4/5-4/7…;

   Input:

   P=pigen()
   print(next(P), next(P), next(P), next(P), sep="\n")

   Output:

   4.0
   2.666666666666667
   3.466666666666667
   2.8952380952380956

4. EJudge: ChainSlice 'Режем лазанью'

   Написать функцию chainslice(begin, end, seq0, seq1, …), которая принимает не менее трёх параметров: два целых числа и не менее одной последовательности. Рассмотрим последовательность seq, образованную всеми элементами seq0, затем — всеми элементами seq1, и т. д. Вернуть эта функция должна итератор, пробегающий элементы последовательности seq с №begin до №end-1 включительно.

   Input:

   print(*(chainslice(17, 33, range(7),  range(8),  range(6),  range(9),  range(5))))

   Output:

   2 3 4 5 0 1 2 3 4 5 6 7 8 0 1 2

Д/З мне:

•  I = iter(Seq)
   old = next(I)
   for new in I:
    ...

вместо

•    1  old = Seq[0]
     2  for new in Seq[1:]:
     3   ...