О принадлежности точки многоугольнику

Статья не дописана — однако уже сейчас в ней есть полезная информация! ☺ -- FrBrGeorge 2022-11-04 18:20:16

В школьной «продвинутой» информатике или просто в задачках, где надо немного повычислять, нередко бывает нужно проверить, принадлежит ли точка треугольнику, или выпуклому многоугольнику, или даже невыпуклому. Обычно на ум приходят алгоритмы, связанные с вычислением положения точки относительно прямой, или с пересечением отрезков, что на поверку оказывается не столько сложно, сколько муторно и сопровождается многочисленными подводными камнями, вроде деления на ноль при составлении уравнения прямой.

Между тем есть довольно надёжный метод определить, лежит ли точка в многоугольнике или за его пределами: надо посчитать сумму углов, образуемых этой точкой в качестве центра и вершинами каждой из сторон многоугольника, с учётом направления (скажем, против часовой стрелки — положительное значение, против — отрицательное). Если сумма углов будет 360° — точка принадлежит многоугольнику, а если 0 — нет.

Не вполне понятно, как определить, в какую сторону — по часовой стрелке или против — мы движемся, перечисляя стороны многоугольника, но от этого зависит только знак результата, преспокойно возьмём модуль. Единственное, что надо соблюдать, — это последовательность вершин при выборе очередной стороны. Например, если отрезки AB и BC — это смежные стороны многоугольника, а O — искомая точка, то считать надо углы AOB+BOC или COB+BOA, но не AOB+COB, и не BOC+BOA.

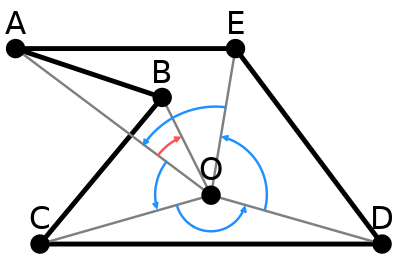
Этот метод работает даже для невыпуклых многоугольников! Да, некоторые углы окажутся с другим знаком, но это не повлияет на окончательный результат — для внутренней точки всё равно надо будет пройти полный оборот, а для внешней — вернуться обратно.

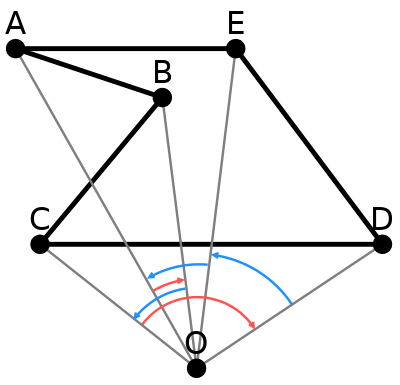
Стоит заметить, что угол, образованный искомой точкой и вершинами стороны — с учётом направления — изменяется в диапазоне от $$-\pi$$ до $$\pi$$, так что напрямую воспользоваться какой-либо обратной тригонометрической функцией у нас не получится: не хватит области значений. Значит, сначала необходимо как-то выяснить направление, а затем применить arccos(), потому что они симметричен относительно знака.

Ещё один вариант — попытаться применить специальную функцию atan2(), область значений которой как раз $$2\pi$$ — учитывается направление угла относительно оси абсцисс. Правда, это не совсем то, что нам нужно: если угол, образуемый искомой точкой и вершинами стороны считать как разность двух atan2(), сумма таких углов будет нулевой независимо от принадлежности точки прямоугольнику!

TODO: может, преобразование какое есть?

Тут появляется идея трюка с векторным произведением. Она проста: в общем случае произведение векторов $$\vec a = (a_x, a_y, a_z)$$ и $$\vec b = (b_x, b_y, b_z)$$ — это вектор $$(a_y b_z - a_z b_y, a_z b_x - a_x b_z, a_x b_y - a_y b_x)$$, перпендикулярный плоскости, которую образуют $$\vec a$$ и $$\vec b$$. В нашем случае оба вектора двумерны, то есть $$(a_x, a_y, 0) \times (b_x, b_y, 0) = (0, 0, a_x b_y - a_y b_x)$$, а значит, у результата только ненулевая только аппликата. Что важно, её знак (направление «от нас» или «на нас», если «глядеть сверху») подчиняется правилу правой руки — отражает направление движения от $$\vec a$$ к $$\vec b$$.

Для выпуклых многоугольников

В случае выпуклого многоугольника задача сильно упрощается: сумму углов считать не надо, достаточно убедиться, что все они одного знака. Просматриваем векторные произведения вида AO × OB, где AB — стороны многоугольника, и если знаки аппликаты одинаковы, то точка внутренняя, а если нет, то внешняя.

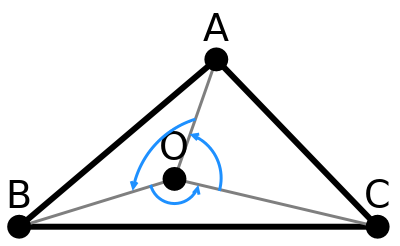
Ещё проще ситуация для треугольников: не нужно даже знать конкретные стороны: подойдёт любая последовательность вершин.

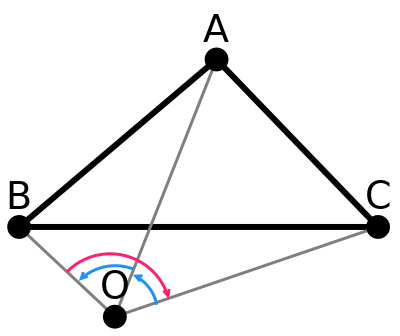
Предположим, нам даны координаты точки O — (x, y) — и координаты вершин треугольника T — (x₀, y₀), (x₁, y₁) и (x₂, y₂). Тогда чтобы проверить O ∈ T, вычислим три «куска» векторных произведений:

• (x₀-x)(y₁-y)-(x₁-x)(y₀-y)

• (x₁-x)(y₂-y)-(x₂-x)(y₁-y)

• (x₂-x)(y₀-y)-(x₀-x)(y₂-y)

и сравним их знаки.

Общая формула

Таким образом, для того, чтобы проверить принадлежит ли точка $$O$$ многоугольнику $$A_1, A_2, \dots, A_n$$, необходимо рассмотреть все углы вида $$\hat{A_1 O A_2}, \hat{A_2 O A_3}, … , \hat{A_{n-1} O A_n}, \hat{A_n O A_1}$$, и для каждого угла $$\hat{A O B}$$ из них:

• Определить направление с помощью знака аппликаты векторного произведения:

  • $$ dir = sign((A_x-O_x)(B_y-O_y) - (A_y-O_y)(B_x-O_x))$$

• Вычислить угол (например, по теореме косинусов)

  • $$ \angle = dir * arccos((|AO|^2+|OB|^2+|AB|^2)/(2|AO|*|OB|)) $$

После чего сложить все получившиеся углы. Если модуль результата окажется в районе $$2\pi$$, точка принадлежит многоугольнику, если в районе нуля — нет. Вряд ли результат будет строго равен нулю из-за погрешности вычислений.

Положение точек относительно прямой

С помощью векторного произведения можно определить и взаимное положение точек A и B относительно прямой, образованной отрезком CD. Если углы CAD и CBD имеют одинаковый знак, точки лежат в одной полуплоскости, если разный — в разных.

TODO

Утверждение

(пока не доказано, но представляется мне истинным). Два треугольника не пересекаются тогда и только тогда, когда у одного из них есть такая сторона, что не принадлежащая ей точка этого треугольника лежит в одной полуплоскости, а все точки второго треугольника — в другой.

Не исключено, что в процессе доказательства выяснится, что оно же верно и для выпуклых многоугольников.