|
Размер: 10475
Комментарий:
|
Размер: 10477
Комментарий:
|
| Удаления помечены так. | Добавления помечены так. |
| Строка 62: | Строка 62: |
| * Количество замеров: график функции `f(x)` на интервале `[a,b]` * — это ломаная, которая начинается в точке `(a,f(a))`, а заканчивается в точке `(b, f(b))`. * Если в ней `N` вершин, то отрезков в ней `N-1`. |
* Количество замеров: график функции `f(x)` на интервале `[a,b]` * — это ломаная, которая начинается в точке `(a,f(a))`, а заканчивается в точке `(b, f(b))`. * Если в ней `N` вершин, то отрезков в ней `N-1`. |
| Строка 159: | Строка 159: |
| * Использование конструкции `range(len(graphX))` наводит на мысль, что так можно было не делать. Действительно, можно было воспользоваться [[py3doc:functions.html#zip]]: | * Использование конструкции `range(len(graphX))` наводит на мысль, что так можно было не делать. Действительно, можно было воспользоваться [[py3doc:functions.html#zip|zip()]]: |
| Строка 165: | Строка 165: |
| * Работа с `eval()` | * Работа с `eval()` |
Построение графика функции
Разбор Д/З
Про графики
Базовая статья: FrBrGeorge/PythonScaleAndRotate
- Что такое график?
- Отображение точек x:f(x)
- ⇒ f(x) должно ∃
Ограничения по началу и концу (не бесконечный, а от A до

- Количество точек в графике? Бесконечно много!
- ⇒ отрезки, а не непрерывная кривая
- ⇒ ломаная (N точек, N-1 отрезок)
- Черепашка и график синуса
- Повторение: циклический конструктор списка:
[ выражение for имя in последователоьность ] или [ выражение for имя, имя in последователоьность_пар] и т. п. Например, [i*2+1 for i in range(6)] - Подготовим черепашье поле
- Точки — это пары координат (x, y)
- График — это последовательность таких пар, например
- Попробуем нарисовать график синуса:
- Фигня какая-то: волняшки слишком частые, но слишком невысокие
- Масштаб по X и Y:
- Но это уже непонятно чего график. В каких границах?
- Повторение: циклический конструктор списка:
Попробуем разобраться
В следующих примерах окно python3 не надо закрывать, иначе придётся заново импортировать math, turtle и определять функции drawgraph() и scale()
Ну, или положить код в файл ![]()
- График как список координат
- В заборе 10 досок, значит, в нём 9 щелей!
Количество замеров: график функции f(x) на интервале [a,b]
— это ломаная, которая начинается в точке (a,f(a)), а заканчивается в точке (b, f(b)).
Если в ней N вершин, то отрезков в ней N-1.
Абсциссы вершин находятся на равном расстоянии друг от друга, т. е. на расстоянии (b-a)/(N-1)
Допустим, вершин у нас 10, значит, отрезков 9; допусти также, что a=-6, b=3
Расстояние между абсциссами (3-(-6))/9 == 1
абсцисса 0-й вершины — начало интервала, a, т. е. -6
абсцисса 1-й вершины — начало отрезка + первый отрезок, т. е a+(b-a)/(N-1), т. е. -6+1*1 == -5
абсцисса 2-й вершины — начало отрезка + первых два отрезка, т. е a+2*(b-a)/(N-1), т. е. -6+2*1 == -4
- …
абсцисса 8-й (№ N-2) вершины — a+(N-2)*(b-a)/(N-1), т. е. -6+8*1 == 2
абсцисса 9-й (№ N-1) вершины — a+(N-1)*(b-a)/(N-1), т. е. -6+9*1 == 2 (т. е. b)
Соответственно, значения функции f(x) в этих точках (предположим, f — это sin):
- Функция масштабирования+переноса (да, это аффинные преобразования, только никому не говорите, а то испугаются).
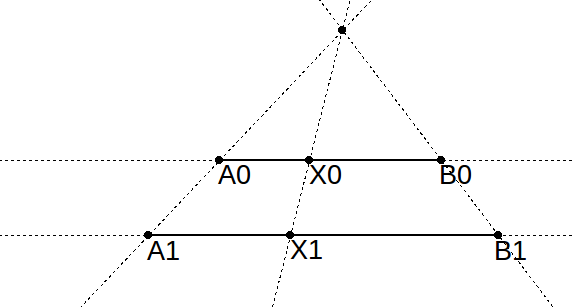
(см. статью) Чтобы превратить точку x0 из диапазона a0,b0 в точку x1 из диапазона a1,b1, надо:
составить пропорцию x0 делит отрезок a0,b0 в той же пропорции, что и x1 делит отрезок a1,b1
т. е. (x0-a0)/(b0-a0) = (x1-a1)/(b1-a1)
и x1 = (x0-a0)/(b0-a0)*(b1-a1)+a1
Напишем функцию scale(), которая это вычисляет:
То есть список из N штук x-координат точек графика можно представить как scale() счётчика i из диапазона 0,N-1 в диапазон a,b:
- Координаты исходного графика vs координаты на экране
Таким образом, в исходном графике функции f(x) x-коорднаты меняются в заданном интервале, а x-координаты — в пределах области значений функции f(x) на этом интервале. Диапазон по x мы задаём, а вот диапазон по y, он же f(x) придётся поискать среди значений функции в точках графика
- Обратите внимание на то, что диапазон оказался близок, но не равен диапазону «настоящего» синуса (-1 … 1; а почему не равен?)
- Что касается координат на экране, то они совсем другие. Они зависят от размеров окна (минус размер рамки)
1 >>> reset() 2 >>> window_width() 3 800 4 >>> window_height() 5 900 6 >>> Border = 20 # Отступ от края окна 7 >>> Left, Right = -window_width()/2+Border, window_width()/2-Border 8 >>> Bottom, Top = -window_height()/2+Border, window_height()/2-Border 9 >>> Left, Right, Bottom, Top 10 (-380.0, 380.0, -430.0, 430.0) 11 >>> for x in Left, Right: 12 for y in Bottom, Top: 13 goto(x,y) 14
Всё готово. Нам нужно нарисовать на экране, координаты которого меняются от Left до Right по x и от Bottom до Top по y, график функции f(x) на n точках в диапазоне от a до b, зная, что f(x) на этом диапазоне принимает значения от miny дол maxy.
- вычислим координаты точек на экране и нарисуем график!
Замечание: надо было сначала переместиться на нулевую точку графика в режиме penup()
Использование конструкции range(len(graphX)) наводит на мысль, что так можно было не делать. Действительно, можно было воспользоваться zip():
TODO
Работа с eval()
Д/З
Внезапно — ничего из учебника, TODO про масштабирование и графики-ломаные — где?
- Про черепашку
TODO
- Ввести отрезок, количество точек и ширину экрана, вывести абсциссы точек на экране
Ввести отрезок, количество точек, а также строку — функцию от x (например, x*sin(x**2)), вывести координаты исходных точек графика
Ввести отрезок, количество точек, ширину и высоту экрана, а также строку — функцию от x (например, x*sin(x**2)), вывести координаты точек графика на экране
- Нарисовать всё это черепашкой
- Нарисовать оси координат
- Что делать, если оси координат лежат в стороне от графика, а рисовать их надо?